Definitie:Data fiind o multime
 , punctul
, punctul  se numeste punct de
acumulare al multimii D daca in orice
vecinatate V a lui x0 au loc
se numeste punct de
acumulare al multimii D daca in orice
vecinatate V a lui x0 au loc  Ø.
Ø.
Definitie
: Fie 
 , o functie si
, o functie si  un punct de acumulare
al multimii D.
un punct de acumulare
al multimii D.
Spunem ca  este
limita functiei f in punctul
este
limita functiei f in punctul  si scriem
si scriem  f(x) = l, daca
f(x) = l, daca
pentru
orice vecinatate V a lui l, exista o vecinatate U a lui  astfel inc@t
pentru
astfel inc@t
pentru
orice  au loc
au loc  (definitia cu vecinatati).
(definitia cu vecinatati).
Teorema 1 (de caracterizare a
limitei unei functii intr-un punct):
Daca  ,
,  si
si  este un punct de
acumulare al multimii D,
este un punct de
acumulare al multimii D, 
atunci
sunt echivalente afirmatiile:
a)  f(x) = l (
f(x) = l ( )
)
b)
Oricare ar fi  , exista
, exista  astfel inc@t pentru
orice
astfel inc@t pentru
orice  cu
cu
proprietatea  sa rezulte
sa rezulte ( definitia cu
( definitia cu  ).
).
Teorema 2 (de caracterizare a
limitei fu 20320h714u nctiei intr-un punct):
Daca  ,
,  si
si  este un punct de
acumulare al multimii D,
este un punct de
acumulare al multimii D,
urmatoarele
afirmatii sunt echivalente:
a)  f(x) = l (
f(x) = l ( )
)
b) Oricare ar fi sirul ( )
) ,
,  cu
cu 
 atunci
atunci

 (definitia
cu siruri).
(definitia
cu siruri).
Observatie
: Daca exista,
limita unei functii intr-un punct este unica.
Observatie
: O functie  ,
,  nu are limita in
punctul
nu are limita in
punctul  , punct de acumulare
, punct de acumulare
al
multimii D, daca exista doua siruri 
 ,
, 
 ,
,  ,
,
 cu
cu 
 ,
, 
 astfel inc@t exista
una din situatiile:
astfel inc@t exista
una din situatiile:
a) unul
din sirurile 
 ,
, 
 nu are limita
nu are limita
b) exista
 f(
f( ) =
) =  ,
,  f(
f( ) =
) =  dar
dar  .
.
Exemplu
: Functia lui Dirichlet  , f(x) =
, f(x) = nu au limite in nici un punct.
nu au limite in nici un punct.
Solutie : Fie  un punct de acumulare
pentru R. Consideram un sir
un punct de acumulare
pentru R. Consideram un sir  si
si
 = 1 = 1. Consideram
un sir �
= 1 = 1. Consideram
un sir � ), si
Atunci
EMBED Equation.3 . Cum
EMBED Equation.3 rezulta conform observatiei anterioare ca functia nu
are limita in punctul
 .
.
B. Limite laterale .
Definitie
: 1) Fie functia  punct de acumulare pentru multimea
punct de acumulare pentru multimea
 . Spunem ca numarul
. Spunem ca numarul  este limita la st@nga
a functiei f in
este limita la st@nga
a functiei f in
punctul
 daca restrictia lui f
la
daca restrictia lui f
la  are limita in punctul
are limita in punctul  si este egala cu
si este egala cu  .
.
2) Fie functia  punct de acumulare
pentru multimea
punct de acumulare
pentru multimea
 . Spunem ca numarul
. Spunem ca numarul  este
limita de dreapta a functiei f in
este
limita de dreapta a functiei f in
punctul
 daca restrictia lui f
la
daca restrictia lui f
la  are limita in punctul
are limita in punctul  si este egala cu
si este egala cu  .
.
 Notatie :
Notatie :  =
=  f(x) =
f(x) =  f(x) = f(
f(x) = f( )
)
Teorema
: Fie functia  si
si  punct de acumulare al
multimii D' cu proprietatea ca
punct de acumulare al
multimii D' cu proprietatea ca
functia
f are limite laterale in EMBED Equation.3 . Atunci sunt echivalente
afirmatiile:
a)functia are limita in punctul
EMBED Equation.3
b) EMBED Equation.3 .
{n aceste
conditii EMBED Equation.3  EMBED Equation.3 .
EMBED Equation.3 .
C.
C.Proprietati ale limitelor de
functii. Operatii cu limite de functii.
1)
1)Daca f(x) = l atunci
EMBED Equation.3  EMBED Equation.3
EMBED Equation.3
Fie
EMBED Equation.3
punct de acumulare al multimii D. Daca exista f(x) EMBED Equation.3 g(X) si exista o vecinatate V a
lui EMBED Equation.3 astfel
inc@t EMBED Equion.3  atunci
atunci 
2)
Fie  punct de acumulare al
multimii D. Daca exista
punct de acumulare al
multimii D. Daca exista  si exista o vecinatate
V a lui
si exista o vecinatate
V a lui  astfel inc@t
astfel inc@t  ,
,  atunci exista
atunci exista  (Criteriul cleste).
(Criteriul cleste).
3)
Daca  ,
,  atunci exista o vecinatate
V a lui
atunci exista o vecinatate
V a lui  astfel inc@t
astfel inc@t
4)
Criterii de majorare : Fie functiile un punct de acumulare al
un punct de acumulare al
multimii D':
a)
Daca si exista
si exista  si V o vecinatate a
lui
si V o vecinatate a
lui  astfel inc@t
astfel inc@t
 atunci
atunci

b)
Daca  atunci
atunci
 .
.
c)
Daca  si exista M>0 astfel inc@t
si exista M>0 astfel inc@t  atunci
atunci  ;
;
d)
Daca  si exista o vecinatate
V a lui
si exista o vecinatate
V a lui  , astfel inc@t
, astfel inc@t  ,
,  atunci
atunci  .
.
e)
Daca  si exista o vecinatate
V a lui
si exista o vecinatate
V a lui  , astfel inc@t
, astfel inc@t  ,
,  atunci
atunci  .
.
5)
Fie functiile  un punct de acumulare al multimii D,
un punct de acumulare al multimii D,  , au sens operatiile:
, au sens operatiile:  +
+ ,
,  -
- ,
, 
 ,
, /
/ ,
, si f(x)+g(x),
si f(x)+g(x),
f(x)-g(x),
f(x)g(x), f(x) / g(x), pentru  si
si  ,
,
- daca in plus
exista o vecinatate V a lui  astfel inc@t
astfel inc@t 
atunci  .
.
Cazuri exceptate: 
Operatii simbolice:
6)
Fie functiile  un punct de acumulare
al multimii A. Daca
un punct de acumulare
al multimii A. Daca
exista  este punct de
acumulare al multimii B, exista o vecinatate V
este punct de
acumulare al multimii B, exista o vecinatate V
al lui  astfel inc@t
astfel inc@t  si exista o
si exista o  , atunci
, atunci
functia are limita in punctul
are limita in punctul  si
si  .
.
D.
Limitele unor functii uzuale
1) Functii polinomiale: 
-
Daca 
-

-

2) Functii rationale :
-

-

3) Functia radical: Pentru  si
si  punct de
punct de
acumulare:
-  -
- 
Pentru 
-
 atunci
atunci 
-

4) Functii trigonometrice:
Pentru 
Pentru 
Pentru 
Pentru 
Pentru 
Pentru 
Pentru 
Pentru 
5) Functia exponentiala: 
-

Pentru
 Pentru
Pentru 
6) Functia logaritmica: 
- 
Pentru 
Pentru 
7) Daca r>0 si functia  este
functia exponentiala de baza e, atunci functia
este
functia exponentiala de baza e, atunci functia  este compunerea celor
doua functii:
este compunerea celor
doua functii:
 si
se numeste functia putere.
si
se numeste functia putere.
- 
- 
- 
E.
Limite remarcabile :
1) 
2)  3)
3) 
4)  5)
5) 
6)  7)
7) 
Daca si daca exista o vecinatate V a lui
si daca exista o vecinatate V a lui  astfel inc@t
astfel inc@t 
atunci
:
1) 
2) 
3)  4)
4) 
Daca  atunci: 5)
atunci: 5) 
6)  7)
7) 
Observatie : Aceste
limite remarcabile sunt utile atunci c@nd apar cazuri de nedeterminare.
F. Asimptote : Fie functia  punct de acumulare
pentru D.
punct de acumulare
pentru D.
Definitie: 1) Spunem ca dreapta
de ecuatie  este
asimptota verticala la st@nga a lui f daca
este
asimptota verticala la st@nga a lui f daca
 sau
sau

2) Spunem ca dreapta de ecuatie
 este
asimptota verticala la dreapta a lui f daca
este
asimptota verticala la dreapta a lui f daca
 sau
sau

3) Spunem ca dreapta de ecuatie
 este asimptota
verticala a lui
f daca este asimptota
este asimptota
verticala a lui
f daca este asimptota
verticala
la st@nga sau la dreapta a lui f sau de ambele parti.
Observatii: 1) Pentru existenta
asimptotei verticale nu este necesar ca f sa fie definita in  .
.
Daca  este
punct de acumulare pentru f atunci functia nu are asimptota verticala
este
punct de acumulare pentru f atunci functia nu are asimptota verticala
 .
.
2) Functia polinomiala fiind
continua pe R, nu are asimptote verticale.
3) Functia rationala are ca
asimptote verticale dreptele  , unde
, unde  este radacina a
este radacina a
numitorului.
4) Functia logaritmica  are ca asimptota
are ca asimptota
verticaladreapta
de ecuatie x = 0.
5) Functia f(x) = tg x are ca asimptote verticaledreptele de ecuatie
Definitie: Fie functia  , unde D contine un interval de forma
, unde D contine un interval de forma  . Spunem ca
. Spunem ca
dreapta
de ecuatie y = mx + n este asimptota oblica la ramura spre  a functiei f, daca
a functiei f, daca
distanta
dintre dreapta si grafic, masurata pe verticala tinde catre zero c@nd x tinde catre

adica
daca: 
Definitie: Fie functia  , D contine un
interval de forma
, D contine un
interval de forma  . Spunem ca
. Spunem ca
dreapta
y = m'x + n' este asimptota oblica la ramura spre  a functiei f daca
a functiei f daca
Teorema: 1) Dreapta de ecuatie
y = mx + n este asimptota oblica la ramura spre  a lui f daca si numai
daca
a lui f daca si numai
daca  (finite) unde
(finite) unde 
2) Dreapta de ecuatie y = m'x +
n' este asimptota oblica la ramura spre  a lui f daca si
a lui f daca si
numai
daca  (finite) unde
(finite) unde 
Observatii: 1) Practic pentru a
determina asimptota oblica la  parcurgem etapele :
parcurgem etapele :
-
se calculeaza  ;
;
-
daca nu este finit, atunci se calculeaza  ;
;
-
daca n este
finit, atunci dreapta de ecuatie y = mx + n este asimptota oblica spre  .
.
Pentru
determinarea asimptotei oblice spre  se procedeaza analog.
se procedeaza analog.
2) Daca cel putin una dintre
cele doua limite nu exista sau este infinita, atunci
nu exista
asimptota
oblica spre  pentru f.
pentru f.
3) Daca m=0 si n este finit, atunci y=n si se numeste asimptota orizontala
spre  a lui f.
a lui f.
Daca m=0 si n' este finit, atunci y=n' si se numeste asimptota orizontala
spre  a lui f.
a lui f.
Observatie: O functie nu poate
admite at@t asimptote oblice c@t si asimptote orizontale la  .
.
Exemple:
A.
1) Sa se
arate ca  nu exista.
nu exista.
Solutie: Consideram functia  este punct de
acumulare al
domeniului de definitie. Consideram sirurile
este punct de
acumulare al
domeniului de definitie. Consideram sirurile  . Dar
. Dar  si
si  . Cum
. Cum  rezulta ca
rezulta ca  nu exista.
nu exista.
Exercitii propuse: Sa se arate ca urmatoarele
limite nu exista: a)  ; b)
; b)  ;
;
c)
Limitele
laterale nu sunt egale, rezulta  nu exista.
nu exista.
2) Sa se determine  astfel inc@t functia
astfel inc@t functia  cu
cu sa aiba limita in punctul x=3.
sa aiba limita in punctul x=3.
Solutie: Daca f are limita in
x=3 => f(3-0)=f(3+0)
Exercitii propuse:
1) Stabiliti daca urmatoarele functii au
limite in punctul indicat:
a)

b)

c)

d)
 e)
e) 
2) Determinati constanta  pentru care functiile
au limita in punctul indicat:
pentru care functiile
au limita in punctul indicat:
a)

b)

c)

B.
1) Sa se calculeze limitele:
a)

trecem la limita
in inegalitate:
b)
 Consideram functia
f(x)=cos x ;
Consideram functia
f(x)=cos x ; ;
; 
Exercitii propuse: Calculati
limitele:
C.
Sa se calculeze limitele:
1)
a)  b)
b) 
c) 
 d)
d) 
e)  f)
f) 
7) a)  b)
b) 
Exercitii propuse: Calculati
urmatoarele limite:
D.
Calculati limitele:
1) a)  b)
b) 
 c)
c) 
 d)
d) 
 e)
e)
 . Notam
. Notam
Exercitii propuse: Calculati limitele:
2) a)  b)
b) 
 c)
c) 
Exercitii propuse: 
 .
.
3) a)  b)
b) 
 c)
c) 
Exercitii propuse: 
4) a)  b)
b) 
 c)
c) 
d)  e)
e)

 Exercitii propuse:
Exercitii propuse:  .
.
Cazuri de nedeterminare
Reamintim,
cazurile de nedeterminare sunt: 
I. Cazul  poare fi int@lnit in
situatiile:
poare fi int@lnit in
situatiile:
a) limite de functii rationale in
puncte finite  .
.
 , daca
, daca  este radacina de ordin
k pentru q se face simplificarea fractiei
este radacina de ordin
k pentru q se face simplificarea fractiei
b) limitele de functii rationale in grupare cu functia
modul.
c) limite de expresii defite
prin c@t de expresii irationale.
- se amplifica cu conjugata
numitorului, numaratorului sau a ambilor.
1) 
2) 
3)
 4)
4) 
 5)
5) 
d) limite de functii
trigonometrice (se utilizeaza limitele: 
 )
)
1)  2)
2) 
 4)
4)
e) limite de functii exponentiale,
logaritmice (se utilizeaza limitele: 
 )
)
1)  2)
2) 
3) 
f) limite de functii care se
calculeaza cu regula lui l'Hospital.
Teorema: Fie  doua functii cu
proprietatile: 1) f,g divizibile prin (a,b) ;
doua functii cu
proprietatile: 1) f,g divizibile prin (a,b) ;
Atunci exista limita  si mai mult
si mai mult 
Exemple: 1)  2)
2)  ;
;
3) 
II. Cazul  poate fi int@lnit in
situatiile:
poate fi int@lnit in
situatiile:
a) limite de functii rationale.
1)  2)
2) 
b) limite de functii irationale,
exponentiale, logaritmice.
1) 
2) 
c) limite de functii care se
calculeaza cu regula lui l'Hospital.
Teorema: Fie  doua functii cu
proprietatile: 1) f,g sunt derivabile pe (a,b);
doua functii cu
proprietatile: 1) f,g sunt derivabile pe (a,b);
2)  3)
3)  4) exista
4) exista
 . Atunci exista limita
. Atunci exista limita  si mai mult are loc egalitatea
si mai mult are loc egalitatea

Exemple: 1)  2)
2) 
 3)
3) 
III. Cazul  :
:
a) limita de functii rationale
(se aduce la acelasi numitor).
b) limite de functii irationale
(se amplifica cu conjugata).
1) 
2) 

3) 

c) limite de functii exponentiale,
logaritmice.
1)  2)
2) 
d) scriem f - g intr-o alta forma:
 sau
sau 
1) 
2) 
IV. Cazul  . Se scrie produsul fg in unul din
urmatoarele moduri:
. Se scrie produsul fg in unul din
urmatoarele moduri:
 daca
daca
 pentru
pentru  sau
sau  daca
daca  , fiecare caz
, fiecare caz
reduc@nduse la cazul  sau
sau  .
.
1)  2)
2) 
 3)
3) 
V. Cazul  . (Se utilizeaza limita
. (Se utilizeaza limita  ).
).
1) 
2) 
3) 
VI. Cazul  . (Se foloseste scrierea
. (Se foloseste scrierea  ).
).
1)  2)
2) 
3)
VII. Cazul  .
.
Limite de functii cu parametri
1) Sa se
determine a,b astfel inc@t 
Solutie:  Daca
Daca  nu are limita 0 atunci
limita va fi
nu are limita 0 atunci
limita va fi  sau
sau  . Obtinem
. Obtinem  si 1-a = 0 =>
a=1.
si 1-a = 0 =>
a=1.
 Obtinem
Obtinem
 .
.
2) Sa se
determine a,b,c astfel inc@t  .
.
Solutie:  .
. 
 Pentru ca limita sa fie finita este necesar ca 2 - 2b = 0 => b=1.
Pentru ca limita sa fie finita este necesar ca 2 - 2b = 0 => b=1.
 Obtinem
Obtinem 
F. Sa se
determine asimptotele pentru functiile:
1) 
- asimptote verticale. Cautam in
 si
si  .
.
=> ca x = -2 este asimptota
verticala a lui f.  + + + + + + + 0 - - -
- - - - 0 + + + + + + +
+ + + + + + + 0 - - -
- - - - 0 + + + + + + +
De asemenea 
 => ca x = 2 este asimptota
verticala a lui f.
=> ca x = 2 este asimptota
verticala a lui f.
- asimptote orizontale.
 y = 1 este asimptota orizontala spre
y = 1 este asimptota orizontala spre
 dreapta
de ecuatie
dreapta
de ecuatie
y = x - 5 este asimptota oblica spre 
3) 
- asimptote verticale: 

dreapta x = 0 este asimptota verticala
la dreapta in 0.
- asimptote orizontale:  ca f nu poseda asimptote orizontale.
ca f nu poseda asimptote orizontale.
- asimptote oblice: - spre 
17)  18)
18) 
II. Determinati parametrii reali a,b,c
astfel in@t sa aiba loc:
1)  ; 2)
; 2)  ;
;
3)
 .
.
III. Determinati asimptotele urmatoarelor functii  , unde D reprezinta domeniul maxim de definitie:
, unde D reprezinta domeniul maxim de definitie:
IV. Se considera functia definita prin expresia
 , a fiind un parametru real, a>0.Sa se determine a astfel inc@t
graficul functiei sa aiba o singura asimptota verticala.
, a fiind un parametru real, a>0.Sa se determine a astfel inc@t
graficul functiei sa aiba o singura asimptota verticala.
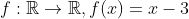 .
.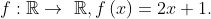
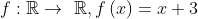 si
si 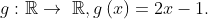
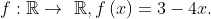
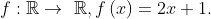
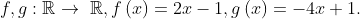
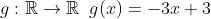
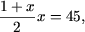
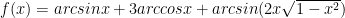

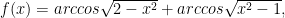




 .
. .
. 
















































 Exercitii propuse
Exercitii propuse



















 2
2






















 .
. 




 => ca x = 2
=> ca x = 2 




 2)
2) 